学习路线
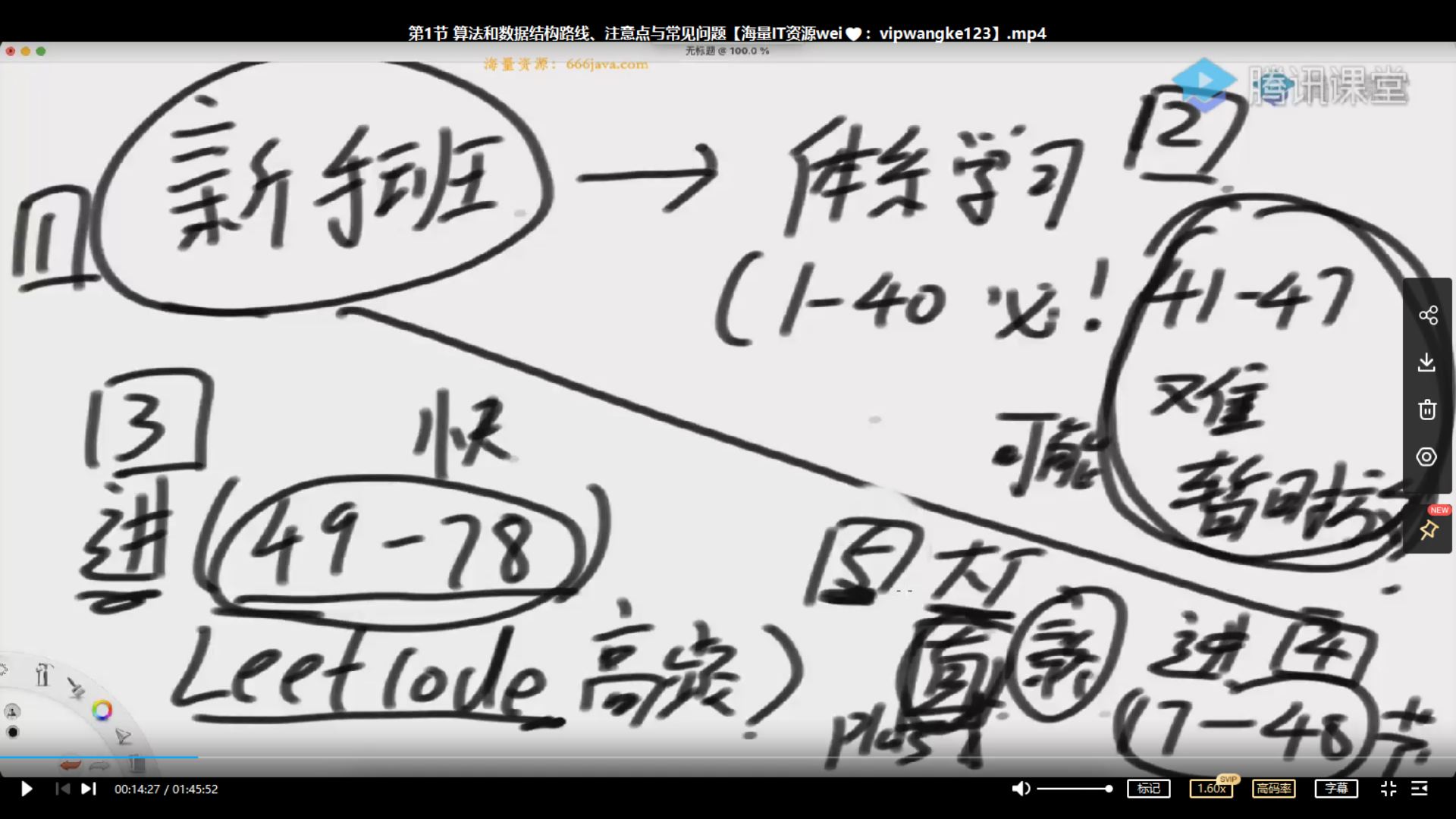
搞定1,2,3差不多达到面试水平
杂记
子问题规模一样的递归可以用Master公式求时间复杂度
T(N) = a * T(N/b) + O(N ^ d);
a:会有几次调用代码
b:每次调用规模的大小
- 如果 log(b , a) < d 时间复杂度为: O(N^d)
- 如果log (b , a) > d 时间复杂度为 : O(N^(log(b,a)))
- 如果log(b , a)== d 时间复杂度为:O(N^d * log(2,n)))
注:log(b,a) 指以b为地a为指数
基础的数据结构
实现栈和队列
用数组实现队列
// 给定一个长度被限制数组空间,如何实现队列?
public class RingArray{
public static class MyQueue{
private int[]arr;
private int pushi;
private int rolli;
private int size;
private final int limit;
public MyQueue(int limit){
arr = new int[limit];
pushi = 0;
polli = 0;
size = 0;
this.limit = limit;
}
public void push(int value){
if(size == limit){
throw new RuntimeException("队列满了,不能再加了");
}
size++;
arr[pushi] = value;
pushi = nextIndex(pushi);
}
public int pop(){
if(size == 0){
throw new RuntimeException("队列空了,不能再拿了");
}
int ans = arr[rolli];
rolli = nextIndex(rolli);
return ans;
}
public boolean isEmpty(){
return size == 0;
}
private int nextIndex(int i){
return i < limit - 1 ? i + 1: 0;
}
}
}数组实现一个特殊的栈,可实时返回栈中最小值
//在基本功能上,再实现返回栈中最小元素的功能,且pop、push、getMin操作的时间复杂度是O(1).
//思路:维护一个栈和一个最小值栈,最小栈中存此时栈中的最小值。
public class GetMinStack {
public static class MyStack {
private Stack<Integer> stackData;
private Stack<Integer> stackMin;
public MyStack2() {
this.stackData = new Stack<Integer>();
this.stackMin = new Stack<Integer>();
}
public void push(int newNum) {
if (this.stackMin.isEmpty()) {
this.stackMin.push(newNum);
} else if (newNum < this.getmin()) {
this.stackMin.push(newNum);
} else {
int newMin = this.stackMin.peek();
this.stackMin.push(newMin);
}
this.stackData.push(newNum);
}
public int pop() {
if (this.stackData.isEmpty()) {
throw new RuntimeException("Your stack is empty.");
}
this.stackMin.pop();
return this.stackData.pop();
}
public int getmin() {
if (this.stackMin.isEmpty()) {
throw new RuntimeException("Your stack is empty.");
}
return this.stackMin.peek();
}
}
}如何用栈实现队列
// 思路:一个push栈,一个pop栈,把push栈的元素放进pop栈再取出来
// 为保证顺序,1、pop栈不为空时,push栈不能往pop栈里倒元素。2、push栈倒元素需要一次性倒完
public class TwoStacksImplementQueue {
public static class TwoStacksQueue {
public Stack<Integer> stackPush;
public Stack<Integer> stackPop;
public TwoStacksQueue() {
stackPush = new Stack<Integer>();
stackPop = new Stack<Integer>();
}
// push栈向pop栈倒入数据
private void pushToPop() {
if (stackPop.empty()) {
while (!stackPush.empty()) {
stackPop.push(stackPush.pop());
}
}
}
public void add(int pushInt) {
stackPush.push(pushInt);
pushToPop();
}
public int poll() {
if (stackPop.empty() && stackPush.empty()) {
throw new RuntimeException("Queue is empty!");
}
pushToPop();
return stackPop.pop();
}
public int peek() {
if (stackPop.empty() && stackPush.empty()) {
throw new RuntimeException("Queue is empty!");
}
pushToPop();
return stackPop.peek();
}
}
}如何用队列实现栈
//实现poll或peek功能是第一个队列中除最后一个元素依次取出加进另一个队列,剩下的那个就是所需要的元素
public class Code07_TwoQueueImplementStack {
public static class TwoQueueStack<T> {
public Queue<T> queue;
public Queue<T> help;
public TwoQueueStack() {
queue = new LinkedList<>();
help = new LinkedList<>();
}
public void push(T value) {
queue.offer(value);
}
public T poll() {
while (queue.size() > 1) {
help.offer(queue.poll());
}
T ans = queue.poll();
Queue<T> tmp = queue;
queue = help;
help = tmp;
return ans;
}
public T peek() {
while (queue.size() > 1) {
help.offer(queue.poll());
}
T ans = queue.poll();
help.offer(ans);
Queue<T> tmp = queue;
queue = help;
help = tmp;
return ans;
}
public boolean isEmpty() {
return queue.isEmpty();
}
}
}堆
public class Heap {
public static class MyMaxHeap {
private int[] heap;
private final int limit;
private int heapSize;
public MyMaxHeap(int limit) {
heap = new int[limit];
this.limit = limit;
heapSize = 0;
}
public boolean isEmpty() {
return heapSize == 0;
}
public boolean isFull() {
return heapSize == limit;
}
public void push(int value) {
if (heapSize == limit) {
throw new RuntimeException("heap is full");
}
heap[heapSize] = value;
// value heapSize
heapInsert(heap, heapSize++);
}
// 返回最大值,并且在大根堆中,把最大值删掉
// 剩下的数,依然保持大根堆组织
public int pop() {
int ans = heap[0];
swap(heap, 0, --heapSize);
heapify(heap, 0, heapSize);
return ans;
}
private void heapInsert(int[] arr, int index) {
// [index] [index-1]/2
// index == 0
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
private void heapify(int[] arr, int index, int heapSize) {
int left = index * 2 + 1;
while (left < heapSize) { // 如果有左孩子,有没有右孩子,可能有可能没有!
// 把较大孩子的下标,给largest
int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
// index和较大孩子,要互换
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
private void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
}排序
选择排序
0~N-1上找到最小值与下标为0的值交换
1~N-1上找到最小值与下标为1的值交换
2~N-1上找到最小值与下标为2的值交换
······
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 0 ~ N-1 找到最小值,在哪,放到0位置上
// 1 ~ n-1 找到最小值,在哪,放到1 位置上
// 2 ~ n-1 找到最小值,在哪,放到2 位置上
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) { // i ~ N-1 上找最小值的下标
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}冒泡排序
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 0 ~ N-1
// 0 ~ N-2
// 0 ~ N-3
for (int e = arr.length - 1; e > 0; e--) { // 0 ~ e
for (int i = 0; i < e; i++) {
if (arr[i] > arr[i + 1]) {
swap(arr, i, i + 1);
}
}
}
}
// 交换arr的i和j位置上的值,i和j是一个位置的话,会出错
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
插入排序
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
// 不只1个数
for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
// i和j是一个位置的话,会出错
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}归并排序
// 递归方法实现
public static void mergeSort1(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
process(arr, 0, arr.length - 1);
}
// 请把arr[L..R]排有序
// l...r N
// T(N) = 2 * T(N / 2) + O(N)
// O(N * logN)
public static void process(int[] arr, int L, int R) {
if (L == R) { // base case
return;
}
int mid = L + ((R - L) >> 1);
process(arr, L, mid);
process(arr, mid + 1, R);
merge(arr, L, mid, R);
}
public static void merge(int[] arr, int L, int M, int R) {
int[] help = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = M + 1;
while (p1 <= M && p2 <= R) {
help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
}
// 要么p1越界了,要么p2越界了
while (p1 <= M) {
help[i++] = arr[p1++];
}
while (p2 <= R) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
}变形1:
给定一个数组,求出每个元素左边比他小的元素之和,再求每个元素左边比他小的元素之和的累加和,要求小于O(N^2)
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return process(arr, 0, arr.length - 1);
}
// arr[L..R]既要排好序,也要求小和返回
// 所有merge时,产生的小和,累加
// 左 排序 merge
// 右 排序 merge
// merge
public static int process(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
// l < r
int mid = l + ((r - l) >> 1);
return
process(arr, l, mid)
+
process(arr, mid + 1, r)
+
merge(arr, l, mid, r);
}
public static int merge(int[] arr, int L, int m, int r) {
int[] help = new int[r - L + 1];
int i = 0;
int p1 = L;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;//就多了这一行代码
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[L + i] = help[i];
}
return res;
}变形2:
求逆序对的数量
给定一个序列有n个数,求n个数中逆序对的个数,逆序对的定义:i < j && a[i] > a[j]。
int merge_sort(int a[], int l ,int r){
//序列只有一个数
if (l == r) return 0;
//递归左边和右边
int mid = l + r >> 1;
int res = merge_sort(a, l , mid) + merge_sort(a, mid + 1, r);
//归并的过程
int i = l , j = mid + 1, k = 0;
while (i <= mid && j <= r){
if (a[i] <= a[j]) t[k++] = a[i++];
else{
t[k++] = a[j++];
res += mid - i + 1;
}
}
while (i <= mid) t[k++] = a[i++];
while (j <= r) t[k++] = a[j++];
//还原数组
for (int i = 0 , j = l ; j <= r ; i ++ , j ++) a[j] = t[i];
return res;
}
变形3:
class Solution {
public static int reversePairs(int[] nums) {
if (nums == null || nums.length < 2) {
return 0;
}
return process(nums, 0, nums.length - 1);
}
public static int process(int[] nums, int l, int r) {
if (l == r) {
return 0;
}
// l < r
int mid = l + ((r - l) >> 1);
return process(nums, l, mid) + process(nums, mid + 1, r) + merge(nums, l, mid, r);
}
public static int merge(int[] nums, int L, int m, int r) {
// [L....M] [M+1....R]
int ans = 0;
int windowR = m + 1;
for (int i = L; i <= m; i++) {
while (windowR <= r && (long) nums[i] > (long) nums[windowR] * 2) {
windowR++;
}
ans += windowR - m - 1;
}
int[] help = new int[r - L + 1];
int i = 0;
int p1 = L;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = nums[p1] <= nums[p2] ? nums[p1++] : nums[p2++];
}
while (p1 <= m) {
help[i++] = nums[p1++];
}
while (p2 <= r) {
help[i++] = nums[p2++];
}
for (i = 0; i < help.length; i++) {
nums[L + i] = help[i];
}
return ans;
}
}堆排序
public class HeapSort{
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) { // O(N)
heapInsert(arr, i); // O(logN)
}
// O(N)
// for (int i = arr.length - 1; i >= 0; i--) {
// heapify(arr, i, arr.length);
// }
int heapSize = arr.length;
swap(arr, 0, --heapSize);
while (heapSize > 0) { // O(N)
heapify(arr, 0, heapSize); // O(logN)
swap(arr, 0, --heapSize); // O(1)
}
}
// arr[index]刚来的数,往上
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
// arr[index]位置的数,能否往下移动
public static void heapify(int[] arr, int index, int heapSize) {
int left = index * 2 + 1; // 左孩子的下标
while (left < heapSize) { // 下方还有孩子的时候
// 两个孩子中,谁的值大,把下标给largest
int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left;
// 父和较大的孩子之间,谁的值大,把下标给largest
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = index * 2 + 1;
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}位运算
int a = 7;
int b = -a = (~a) + 1 = -7;// arr中,只有一种数,出现奇数次
public static void printOddTimesNum1(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
System.out.println(eor);
}
// arr中,有两种数,出现奇数次
public static void printOddTimesNum2(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
// a 和 b是两种数
// eor != 0
// eor最右侧的1,提取出来
// eor : 00110010110111000
// rightOne :00000000000001000
int rightOne = eor & (-eor); // 提取出最右的1
int onlyOne = 0; // eor'
for (int i = 0 ; i < arr.length;i++) {
// arr[1] = 111100011110000
// rightOne= 000000000010000
if ((arr[i] & rightOne) != 0) {
onlyOne ^= arr[i];
}
}
System.out.println(onlyOne + " " + (eor ^ onlyOne));
}
// 输入一定能够保证,数组中所有的数都出现了M次,只有一种数出现了K次
// 1 <= K < M
// 返回这种数
public static int km(int[] arr, int k, int m) {
int[] help = new int[32];
for (int num : arr) {
for (int i = 0; i < 32; i++) {
help[i] += (num >> i) & 1;
}
}
int ans = 0;
for (int i = 0; i < 32; i++) {
help[i] %= m;
if (help[i] != 0) {
ans |= 1 << i;
}
}
return ans;
}